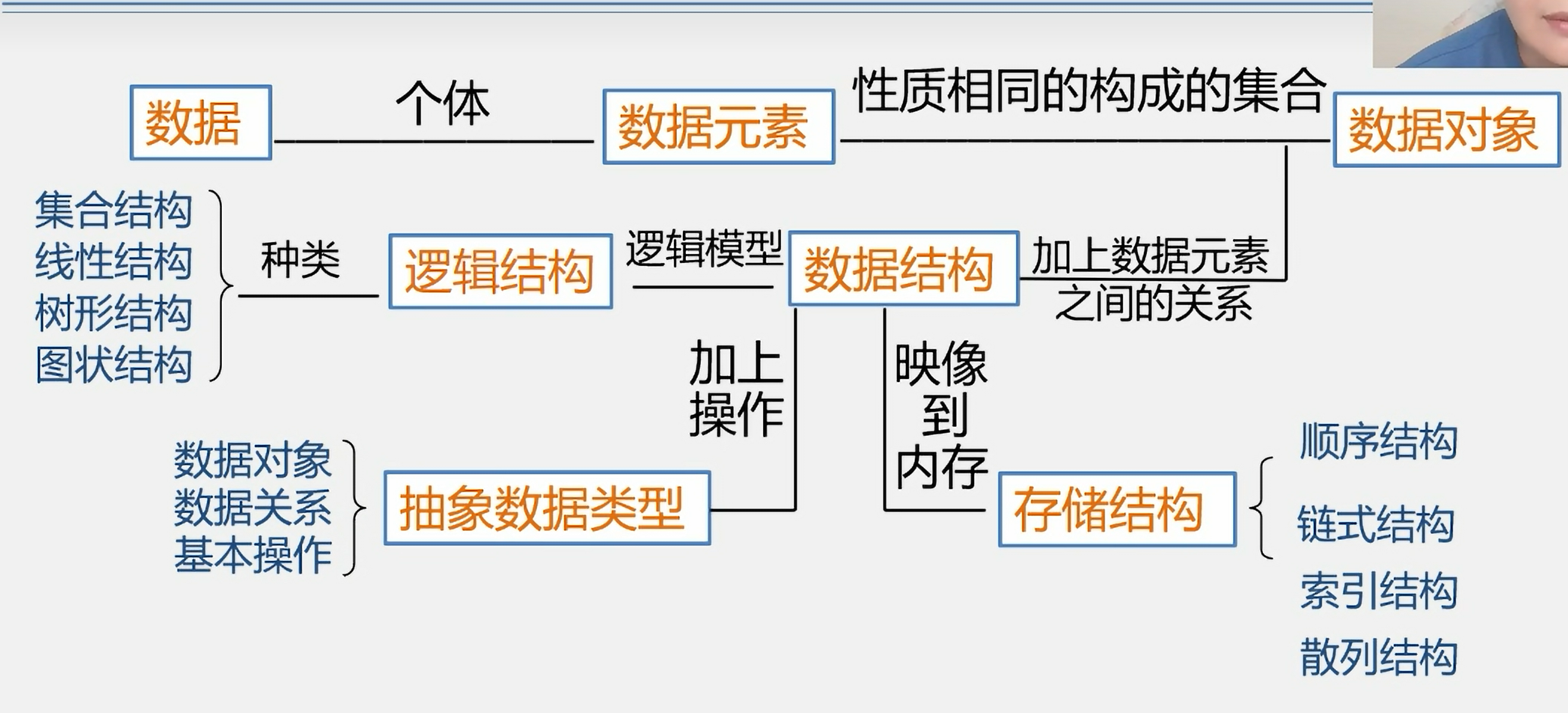
数据结构 一、绪论 (一)数据结构 抽象数据类型的标识和实现:
eg. 抽象复数数据类型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include<iostream> using namespace std; struct Complex { double real; double imag; Complex(double r=0.0,double i=0.0):real(r),imag(i){} double modulus() const { return sqrt(real * real + imag * imag); } }com1,com2; int main() { com2.real=1.0; com2.imag = 2.0; Complex com(1.0,2.0); cout << com.modulus() << endl; cout << com1.modulus() << endl; cout << com2.modulus() << endl; return 0; }
(二)算法 1.算法性质 1)有穷性
2)确定性
3)可行性
4)输入
5)输出
2.算法分析 渐进时间复杂度 (时间复杂度): T(n)=O(f(n))
1.找执行次数最多的那个基本语句
2.计算语句频度->f(n)
3.O(f(n))表示
比较数量级 同量级
渐进空间复杂度: S(n)=O(f(n))
1 2 3 4 5 for(i=0;i<n/2;i++){ t=a[i]; a[i]=a[n-i-1]; a[n-i-1]=t; } //空间复杂度O(1)
1 2 3 4 5 6 7 for(i=0;i<n;i++){ b[i]=a[n-i-1]; } for(i=0;i<n;i++){ a[i]=b[i]; } 空间复杂度O(n)
二、线性表 线性表的定义: 包含若干相同类型数据元素的一个线性序列,记为 $L=(a_0,···,a_{i-1},a_i,a_{i+1},···,a_{n-1})$
线性表的逻辑结构: $L=(D,R)$
对于稀疏多项式造成的大量存储浪费,只记不为零的,记录多个元素$P=((p_1,e_1),(p_2,e_2),···,(p_m,e_m))$
思考:1.数组大小怎么定?
(一)线性表的抽象数据类型 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 //以下不是代码,只是为了方便观看 ADT List{ 数据元素集:D 数据关系集:R 基本操作集:P ListInit(&L) 操作结果:构建一个空的线性表L ListDestory(&L) 初始条件:线性表L存在 操作结果:撤销线性表L ListClear(&L) 初始条件:线性表L存在 操作结果:将L制成一张空表 ListLength(&L) 初始条件:线性表L存在 操作结果:返回L中元素个数(即表长n) ListEmpty(&L) 初始条件:线性表L存在 操作结果:L表为空时返回true,否则返回false GetElem(L,i) 初始条件:线性表L存在,且0≤i≤n 操作结果:返回L中第i个元素的值/指针 LocatedElem(L,e) 初始条件:线性表L存在,且e∈datatype 操作结果:若e存在L中,返回e的序号(或指针),否则返回e不在表中的信息(eg.-1/NULL等) PreElem(L,cur) 初始条件:线性表L存在,且cur∈datatype 操作结果:若cur在L中且不是表头,返回cur的前驱,否则返回NULL SuccElem(L,cur) 初始条件:线性表L存在,且cur∈datatype 操作结果:若cur存在L中且不是表尾元素,返回cur的直接后继的值,否则返回NULL ListInsert(&L,i,e) 初始条件:线性表L存在,且e∈datatype 操作结果:若0≤i≤n-1,将e插入到第i个元素之前,表长增加1,函数返回TURE;若i=n,将e插入到表尾,表长增加1,函数返回TURE;i为其他值时函数返回FALSE,L无变化。 ListDel(&L, i) 初始条件:线性表L存在。 操作结果:若0≤i≤n-1,将第i个元素从表中删除,函数返回TURE,否则函数返回FALSE,L无变化。 ListTraverse(L) 初始条件:线性表L存在。 操作结果:依次对表中的元素利用visit()函数进行访问 }ADT list;
(二)线性表顺序存储结构 定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构
存储位置计算:$LOC(a_{i+1})=LOC(a_1)+(i-1)*l$
优点:随机访问快,可以直接计算数据元素的地址;存储密度大(结点本身所占存储量/节点结构所占存储量)
不足:插入、删除效率低,不利于动态增长;浪费存储空间(数组大小可能会定的很大)
实现(部分):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 #define MAXSIZE 1000 typedef char ElemType; struct SqList { ElemType *elem; //可以typedef char ElemType等等,也可以用结构体,类 // ElemType data[MAXSIZE];//利用malloc等动态分配数组,*elem第一个元素 int length; }; bool ListInit(SqList& L) { L.elem = new ElemType[MAXSIZE]; if (!L.elem){ cerr << "error" << endl; return false; } L.length = 0; return 1; } void ListDestory(SqList& L) { if (L.elem) delete L.elem; } void ListClear(SqList& L) { L.length = 0; } int ListLength(SqList& L) { return L.length; } bool ListEmpty(SqList& L) { return (L.length == 0); } //查找第i个元素 ElemType GetElem(SqList& L,int i) { if (i <= L.length && i >= 1)return L.elem[i - 1]; else return NULL; } //查找e元素的位置 int LocatedElem(const SqList& L, const ElemType& e) { for (int i = 0; i < L.length; ++i) { if (L.elem[i] == e) { return i + 1; } } return 0; //算法时间复杂度:O(n) (n+1)/2 } //插入 bool InsertList(SqList& L, const ElemType& e, const int& i) { if (L.length >= MAXSIZE || i<1 || i>L.length + 1)return false; else if (i <= L.length) { for (int j = L.length - 1; j >= i - 1; j--) { L.elem[j + 1] = L.elem[j]; } } L.elem[i - 1] = e; L.length += 1; return true; //算法时间复杂度:O(n) } //删除 bool ListDel(SqList& L, const int i) { if (i <= 0 || i > L.length || L.length == 0)return false; for (int j = i - 1; j < L.length-1; j++) { L.elem[j] = L.elem[j + 1]; } L.length--; return true; //时间复杂度O(n);(n-1)/2 }
补充:1.C语言动态内存分配
1 2 3 4 5 6 SaList L; L.data=(ElemType*)malloc(sizeof(ElemType)*MaxSize) //加头文件 #include<stdlib.h> //malloc(m)函数,开辟m字节长度的地址空间,并返回这段空间的首地址 //sizeof(x)运算,计算变量x的长度 //free(p)函数,释放指针p所指变量的存储空间,即彻底删除一个变量
2.C++动态存储分配
1 2 int *p1 = new int(10);//申请用于存放T类型对象的内存空间,并依初值列表赋以初值结果值:成功:T类型的指针,指向新分配的内存,失败:0(NULL) delete p1;//释放指针P所指向的内存。P必须是new操作的返回值
3.C++参数传递 省略(值 ;指针变量(可影响也可不影响);引用类型;数组名 )
(三)线性表的链式存储结构 定义:用物理位置任意的存储单元来存放线性表的数据元素
结点(数据+指针)+链表(n个结点由指针链组成)包括:单链表,双链表,循环链表
设头结点的好处:1.便于首元结点的处理 2.便于空表和非空表的统一管理
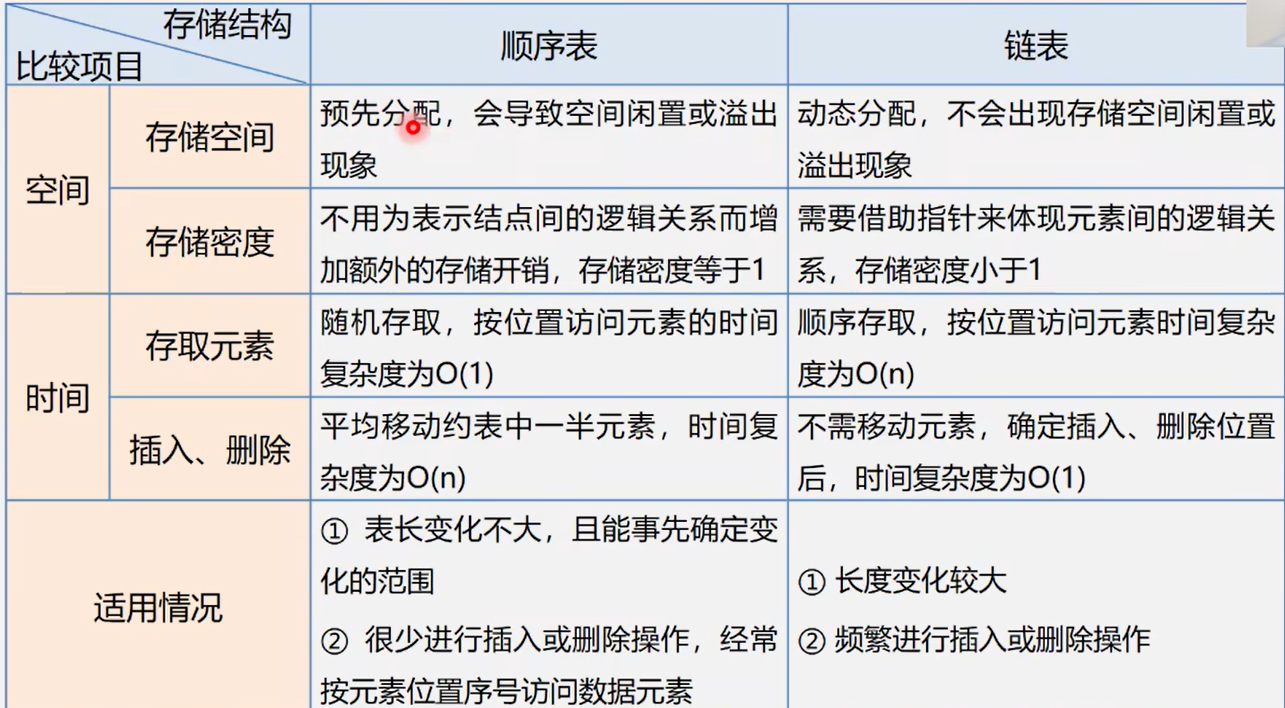
顺序表->随机存取 链表->顺序存取
优点:便于插入、删除和动态增长
劣势:随机访问慢,存储密度小
1.单链表
实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 #include<iostream> using namespace std; /*struct ElemType { char num[8]; char name[8]; int score; };//举例,因省去运算符重载,所以以char类型举例*/ typedef char ElemType; struct Lnode { ElemType data; Lnode* next; }; typedef Lnode *LinkList;//LinkList L;<=>Lnode *L; //重载"=="号 //初始化 bool InitList(LinkList& L) { L = new Lnode; //堆区开辟一个头结点 L->next = nullptr; return true; } //建立单链表——头插法 void CreateList_H(LinkList& L, int n) { L = new Lnode; L->next = NULL; for (int i = n; i >= 1; i--) { LinkList p = new Lnode; cin >> p->data; p->next = L->next; L->next = p; }//O(n) } //建立单链表——尾插法 void CreateList_T(LinkList& L, int n) { L = new Lnode; L->next = NULL; LinkList r = L; for (int i = 1; i <= n; i++) { LinkList p = new Lnode; cin >> p->data; p->next = NULL; r->next = p; r = p;//O(n) } } //判断链表是否为空(空表:链表中没有元素,头节点&指针仍然在(只需要判指针为空)) bool ListEmpty(LinkList L) { if (L->next)return 0; else return 1; } //销毁 void ListDestroy(LinkList& L) { LinkList p; while (L) { p = L; L = L->next; delete p; } } //清空链表 void ListClear(LinkList& L) { LinkList p,q; p = L->next; while (p) { q = p->next; delete p; p = q; } /*q = p->next; delete p; while (q) { p = q; q = q->next; delete p; }错的,对应while里*/ L->next = NULL; } // 链表表长 int GetLength(const LinkList& L) { LinkList p; int cnt = 0; p = L->next; while (p) { cnt++; p = p->next; } return cnt; //O(n) } //取第i个元素 LinkList GetElem(const LinkList& L, const int& i) { LinkList p = L; int cnt = 0; if (i <= 0)return nullptr; while (p->next&&cnt<i) { p = p->next; cnt++; } if (p && cnt == i) { return p; }else return nullptr; } //按值查找(找地址返回p) int LocateElem(LinkList& L, ElemType& e) { Lnode* p = L->next; size_t cnt = 1; while (p) { if (p->data == e) { return cnt; } ++cnt; p = p->next; } return 0;//O(n) } //插入 bool InsertList(LinkList& L, const int& i, const ElemType& e) { LinkList p = L; int j = 0; while (p || j < i - 1) { p = p->next; j++; } if (!p || i < 0)return 0; LinkList s = new Lnode; s -> data = e; s->next = p -> next; p->next = s; return 1;//有查找O(n),没有O(1) } //删除第i个结点 bool DelList(LinkList& L, int& i) { LinkList p; int j = 0; while (p || j < i - 1) { p = p->next; j++; } if (!(p->next) || i < 0 ||!p)return 0; LinkList q; p->next = q->next; delete q; return 1; }
3.单向循环链表 单链表的首尾节点相连
注意:1.条件判断是否等于头指针,而非判断是否为空
1 2 3 //单链表--------------循环链表 //while(p)--------->while(p!=L) //while(p->next)--->while(p->next!=L)
2.两种(1)头指针表示循环链表
(2)尾指针表示循环链表(好处:找$a_1$ $a_n$的时间复杂度均为O(1),表的的操作常在首位位置上进行 )
3.带尾指针循环链表的合并
1>Tb表头连接到Ta表尾
2>释放Tb头节点
1 2 3 4 5 6 7 LinkList Connect(LinkList Ta,LinkList Tb) { p=Ta->next; Ta->next=Tb->next->next; delete Tb->next; Tb->next=p; return Tb; }
4.双向链表
1 p->prior->next = p = p->next->next
实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 #include<iostream> using namespace std; typedef char ElemType; struct DuLnode { ElemType data; DuLnode* next,* prior; }; typedef DuLnode* DuLinkList; //头插 void CreatListHead(DuLinkList& L, const size_t n) { for (int i = 0; i < n; ++i) { DuLnode* p = new DuLnode; cin >> p->data; p->prior = L; p->next = L->next; L->next = p; if (p->next != nullptr) { p->next->prior = p; } } } //尾插 void CreatListTail(DuLinkList& L, const size_t n) { DuLnode* r = L; for (int i = 0; i < n; ++i) { DuLnode* p = new DuLnode; cin >> p->data; p->prior = r; p->next = NULL; r->next = p; r = p; } } //查找第i个元素 DuLinkList GetElemP_DuL(DuLinkList& L, const int i) { DuLinkList p = L; int cnt = 0; if (i <= 0)return nullptr; while (p->next && cnt < i) { p = p->next; cnt++; } if (p && cnt == i) { return p; } else return nullptr; } //插入 bool ListInsert_DuL(DuLinkList& L, const int i, const ElemType& e) { DuLinkList p; if (!(p = GetElemP_DuL(L, i))) return false; DuLinkList s = new DuLnode; s->data = e; s->prior = p->prior; p->prior->next = s; s->next = p; p->prior = s; return true; } //删除 bool ListErase_DuL(DuLinkList& L, const int i) { DuLinkList p; if (!(p = GetElemP_DuL(L, i))) return false; p->prior->next = p->next; p->next->prior = p->prior; delete p; return true; }
5.双向循环链表
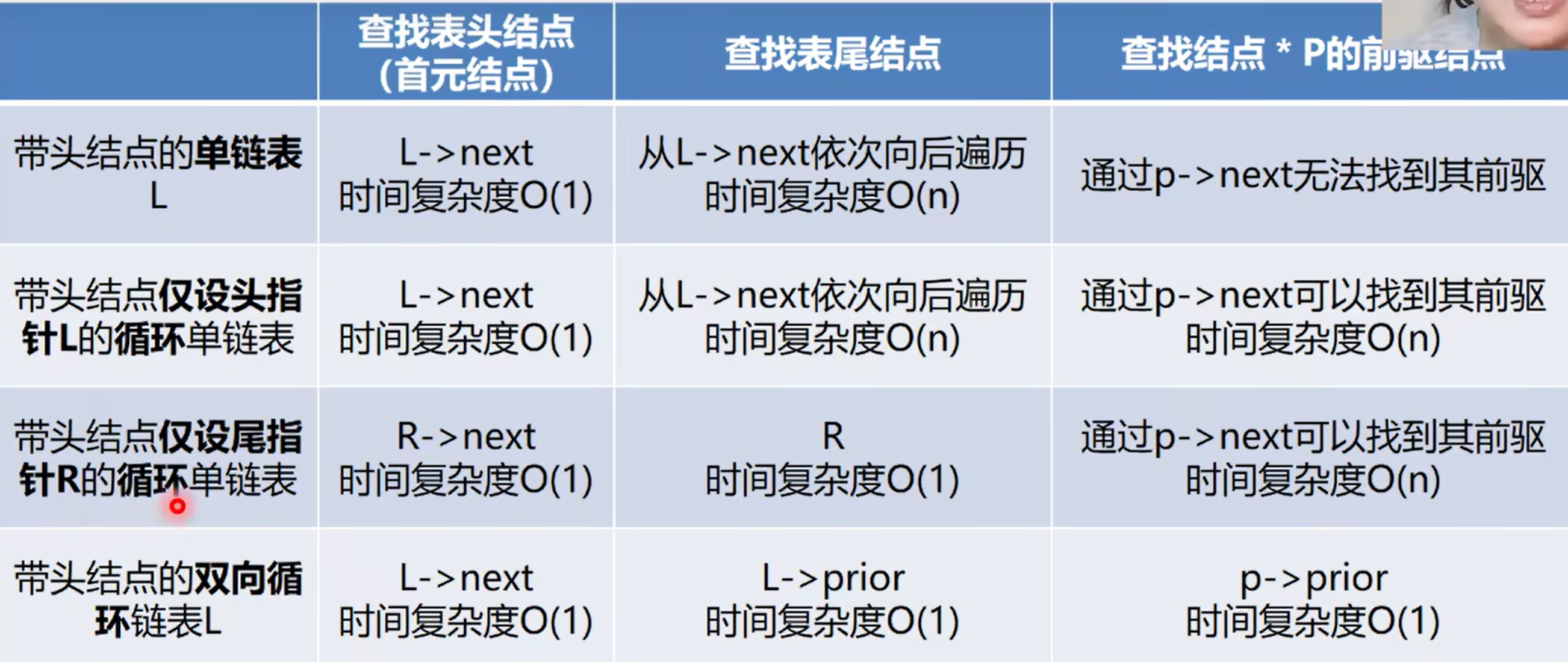
6.总结 (1)
(2)
(四)线性表的应用 1.线性表的合并 1 2 3 4 5 6 7 8 9 10 void union(List& La, List Lb) { Lal = listLength(La); Lbl = ListLength(Lb); ElemType e; for(int i = 0; i < Lb_len; i++) { GetElem(Lb, i,e); if (!LocatedElem(La, e)) Listinsert(&La,++Lal,e);//O(lal*lbl) } }
2.有序表的合并 (顺序表)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void MergeList_Sq(SqList LA, SqList LB, SqList& LC) { ElemType *pa = LA.elem; ElemType *pb = LB.elem; LC.length = LA.length + LB.length; LC.elem = new ElemType[LC.length]; ElemType *pc = LC.elem; ElemType *pa_last = LA.elem + LA.length - 1; ElemType *pb_last = LB.elem + LB.length - 1; while (pa <= pa_last && pb <= pb_last) { if (*pa <= *pb)*pc++ = *pa++; else *pc++ = *pb++; } while (pa <= pa_last)*pc++ = *pa++; while (pb <= pb_last)*pc++ = *pb++; }//O(lal+lbl)
(链式表)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void MergeList_L(LinkList& La, LinkList& Lb, LinkList& Lc) { LinkList pa = La->next; LinkList pb = Lb->next; LinkList pc = Lc = La; while (pa && pb) { if (pa < pb) { pc->next = pa; pc = pa; pa = pa->next; } else { pc->next = pb; pc = pb; pb = pb->next; } } pc->next = pa ? pa : pb; delete Lb;//O(lal+lbl)空间:O(1) }
3.案例 (一元多项式运算—数组)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void PolyOperate(SqList &L1, SqList &L2, SqList &L3) { for (int i = 0; i < L1.length && i < L2.length; ++i) { L3.elem[i] = L1.elem[i] + L2.elem[i]; L3.length += 1; } if (L1.length <= L2.length) { for (int j = L1.length; j < L2.length; ++j) { L3.elem[j] = L2.elem[j]; L3.length += 1; } } else { for (int j = L2.length; j < L1.length; ++j) { L3.elem[j] = L1.elem[j]; L3.length += 1; } } }
(稀疏多项式的运算——顺序表)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 //数组 void PloyOperate(LinkList &La, LinkList &Lb, LinkList &Lc) { Lnode *pa = La->next; Lnode *pb = Lb->next; Lc = La; Lnode *pc = Lc; while(pa && pb) { if(pa->data.index < pb->data.index) { pc->next = pa; pc = pc->next; pa = pa->next; } else if(pa->data.index > pb->data.index) { pc->next = pb; pc = pc->next; pb = pb->next; } else if(pa->data.index == pb->data.index) { pa->data.coef += pb->data.coef; pc->next = pa; pc = pc->next; pa = pa->next; pb = pb->next; } } pc->next = (pa ? pa : pb); delete Lb; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 //链表 struct PNode { float coaf; int expn; struct PNode* next; }; typedef PNode* Ploynomial; //链表 void CreatePolyn(Ploynomial& P, int n) { P = new PNode; P->next = NULL; for (int i = 1; i <= n; i++) { Ploynomial s = new PNode; cin >> s->coaf >> s->expn; Ploynomial pre = P; Ploynomial q = P->next; while (q && (q->expn < s->expn)) { pre = q; q = q->next; } s->next = q; pre->next = s; } } void PloyOperate(Ploynomial& La, Ploynomial& Lb, Ploynomial& Lc) { Ploynomial pa = La->next; Ploynomial pb = Lb->next; Ploynomial pc = Lc = La; while (pa && pb) { if (pa->expn < pb->expn) { pc->next = pa; pa = pa->next; pc = pc->next; } else if (pa->expn == pb->expn) { pa->coaf = pa->coaf + pb->coaf; pc->next = pa; pa = pa->next; pb = pb->next; pc = pc->next; } else { pc->next = pb; pb = pb->next; pb = pb->next; } } pc->next = (pa ? pa : pb); delete Lb; }
(图书信息管理系统)
1 2 3 4 5 6 7 8 9 10 11 12 typedef struct Book { string isbn; string name; float price; } ElemType; struct Lnode { ElemType data; Lnode *next; } *LinkList; //各操作与以上单链表等操作类似
 抽象数据类型的标识和实现:
抽象数据类型的标识和实现: