数据结构|树

五、树

（一）基本概念

1.定义：n个节点构成的一个层次结构（n=0,空树，n>0,只有各个节点，其余节点互不相交）

2.基本术语：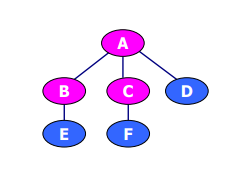

父节点(双亲)与子节点(孩子)
如A是B、C、D的父节点，B、C、D是A的孩子，除根节点外，每个节点有且只有1个父节点
祖先与子孙：如A、B是E的祖先，B、C、D、E、F是A的子孙
兄弟:具有同一父节点，如B、C、D是兄弟

堂兄弟：父节点在同一层
根节点：非空树中无前驱节点的结点，1个，无父节点
叶节点：无子节点
分支节点：其余
节点的入度(ID)：指向节点的分支数目
节点的出度(OD)：子节点数
树的度(TD)：max(所有节点的出度)
如OD(A)=3，OD(B)=1。叶节点的出度为0.
根的入度为0，其它各节点的入度=1.
度=K 的树称为K叉树，但二叉树有特定的定义。
有序树:树中任一节点的各子树从左到右有序
无序树:否则
森林(或树林)：m(m≥0)棵互不相交的有序树的有序集合

3.性质：

树中节点总数n（n≥0）等于树中各节点的出度之和加1 。
度＝K的树（K叉树）第i(i≥1)层至多有Ki-1个节点。
深度＝h(h≥1)的K（K＞1）叉树至多有(Kh-1)/(K-1)个节点。
包含n（n≥0）个节点的K（K＞1）叉树的最小深度为： $\left\lceil \log_K \left( n(K-1) + 1 \right) \right\rceil$

（二）二叉树

1.定义：或者是空树，或者由1个根节点以及左子树和右子树组成，左子树和右子树都是二叉树。

2.特点：区分左右

性质：

二叉树的第i层上至多有$2^{i-1}$个节点（满二叉树），至少得有一个节点
深度为k的二叉树至多有$2^k-1$个节点（k>=1）
设二叉树BT中叶节点数为$n_0$，出度为2的节点数为$n_2$，则有：$n_0=n_2+1$
含有n(n ≥1)个节点的完全二叉树（与满二叉树编号一一对应/除了最后一层外，其余各层的节点都达到了最大数目，且最后一层的所有节点都从左向右连续排列）的深度：$h = \left\lfloor \log_2 n \right\rfloor + 1$2*边 = 入度+出度
编号略

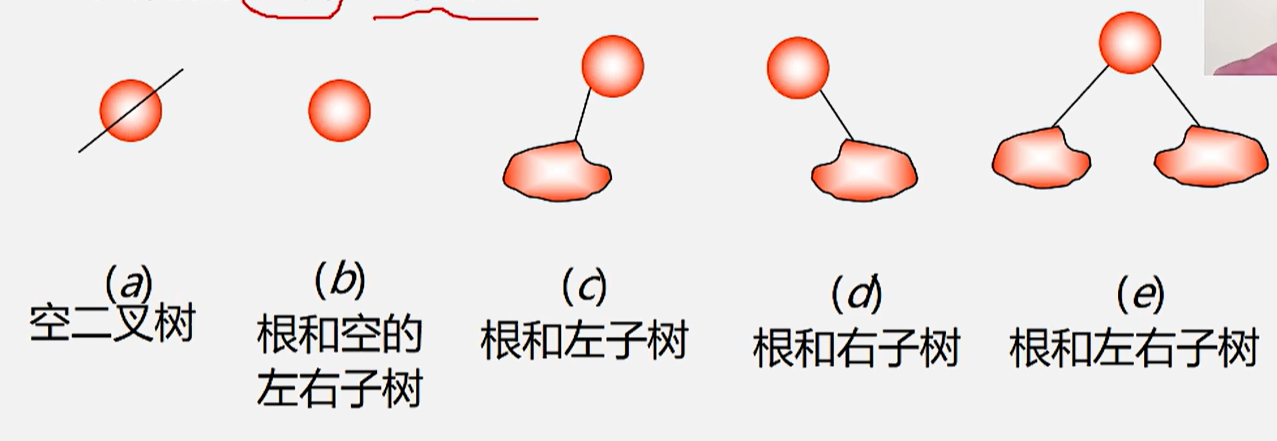
3.五种基本形态：

4.案例

数据压缩问题（编码）、求表达式的解

5.抽象数据类型定义：略

D\R\P

6.存储结构

（1）顺序存储（按满二叉树编号）

优点：简单

缺点：不利于增删改；浪费空间，不适合非完全二叉树

（2）链式存储

二叉链表：

struct BiNode {
    TElemType data;
    BiNode* lchild, * rchild;//n个节点，n+1个空指针域
};
BiNode* BiTree;

三叉链表

struct TriNode {
    TElemType data;
    BiNode* lchild, * rchild,* parent;
};
BiNode* TriTree;

7.遍历二叉树

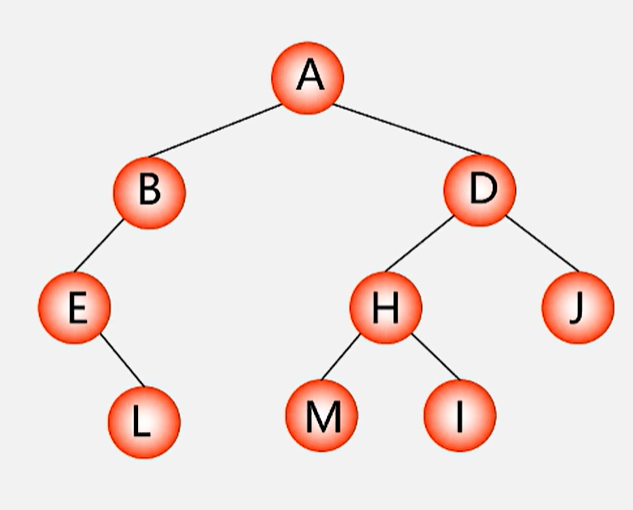
（1）前序遍历（DLR）eg.ABELDHMIJ 前缀表达式（波兰式）

（2）中序遍历（LDR）eg.ELBAMHIDJ 中缀

（3）后序遍历（LRD）eg.LEBMIHJDA 后缀（逆波兰式）

反过来，由序列得到二叉树（先序+中序后序+中序）

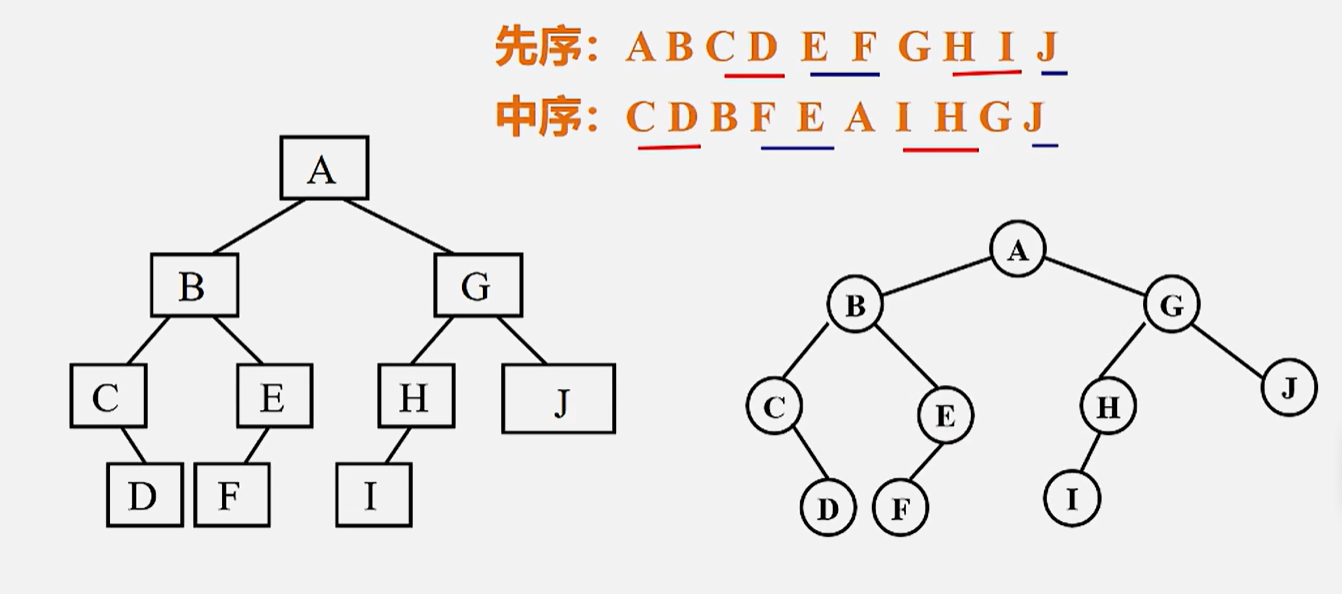
实现：利用二叉链表（每个节点经过三次,三种遍历访问时机不同时间O(n) 空间O(n)）

(1)递归算法

（先序遍历）

bool PreOrderTraverse(BiTree T){
    if (T == Null)return 1;
    else {
        visit(T);
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

（中序遍历）

bool InOrderTraverse(BiTree& T)
{
    if (T == nullptr)
    {
        return true;
    }
    InOrderTraverse(T->lchild);
    visit(T);
    InOrderTraverse(T->rchild);
    return true;
}

（后序遍历）

bool PostOrderTarverse(BiTree& T)
{
    if (T == NULL)return 1;
    else {
        PostOrderTarverse(T->lchild);
        PostOrderTarverse(T->rchild);
        visit(T);
        return 1;
    }
}

（2）非递归算法

（中序遍历）利用栈

bool InOrderTraverse(BiTree T)
{
    BiTree p;
    InitStack(S);
    p = T;
    while (p || !StackEmpty(S))
    {
        if (p) {
            Push(S, p);
            p = p->lchild;
        }
        else {
            Pop(S, q);
            visit(q);
            p=q->rchild;
        }
    }
    return 1;
}

(3) 层次遍历—利用队列

void LevelOrderTraverse(BiTree T)
{
    if (!T)return;
    queue<BiTree> Q;
    Q.push(T);
    while (!Q.empty())
    {
        BiTree p = Q.front();
        Q.pop();
        visit(p);
        if (p->lchild)Q.push(p->lchild);
        if (p->rchild)Q.push(p->rchild);
    }
}

（4）建立二叉树

bool CreatBiTree(BiTree& T)
{
    TElemType input;
    cin >> input;
    if (input == '#')
        return false;
    T = new BiNode;
    T->data = input;
    CreatBiTree(T->lchild);
    CreatBiTree(T->rchild);
    return true;
}

（5）复制二叉树

bool CopyBiTree(const BiTree& T, BiTree& NewT)
{
    if (T == nullptr)
    {
        return false;
    }
    NewT = new BiNode;
    NewT->data = T->data;
    CopyBiTree(T->lchild, NewT->lchild);
    CopyBiTree(T->rchild, NewT->rchild);
    return true;
}

（6）计算二叉树深度

int Depth(BiTree &T)
{
    if(T == nullptr)
    {
        return 0;
    }
    int m = Depth(T->lchild);
    int n = Depth(T->rchild);
    if(m>n)
        return m+1;
    else
        return n+1;
}

（7）计算节点个数

int CountNode(BiTree& T)
{
    if (T == nullptr)
    {
        return 0;
    }
    return CountNode(T->lchild) + CountNode(T->rchild) + 1;
}

（8）计算叶子节点个数

int Count0Node(BiTree& T)
{
    if (T == nullptr)
    {
        return 0;
    }
    if (T->lchild == nullptr && T->rchild == nullptr)
    {
        return 1;
    }
    return Count0Node(T->lchild) + Count0Node(T->rchild);
}

8.线索二叉树

利用空指针域（n+1），左孩子为空，将空左孩子指针域指向其前驱，右->后继

增设两个标志域，ltag，rtag